What is the pitch diameter of a spur gear with 40 teeth and a module of 2.5 mm?
Spur gears are fundamental components in countless mechanical systems, responsible for transmitting power and motion between parallel shafts. Understanding their key dimensions is crucial for proper design, manufacturing, and assembly. Among these dimensions, the pitch diameter stands out as a critical theoretical concept that defines the effective diameter where two gears mesh.
Understanding Key Gear Terminology
Before diving into the calculation, let’s clarify the terms involved:
- Module (m): The module is a standardized unit that defines the size of the gear teeth. It is expressed in millimeters (mm) in the metric system. A larger module indicates larger teeth. The module is the ratio of the pitch diameter to the number of teeth.
- Number of Teeth (Z): This is simply the count of teeth around the gear’s circumference. It directly influences the gear ratio when paired with another gear.
- Pitch Diameter (D): This is the diameter of the pitch circle, which is the theoretical circle on which the gear teeth effectively mesh with the teeth of another gear. It’s an imaginary line but critical for determining the center distance between mating gears.
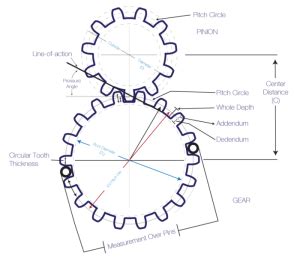
The Formula for Pitch Diameter
The relationship between pitch diameter, module, and the number of teeth is straightforward and fundamental in gear design. The formula to calculate the pitch diameter (D) is:
D = m × Z
Where:
- D = Pitch Diameter (in millimeters)
- m = Module (in millimeters)
- Z = Number of Teeth

Step-by-Step Calculation
Given the problem, we have the following values for our spur gear:
- Number of Teeth (Z) = 40
- Module (m) = 2.5 mm
Now, let’s apply the formula:
D = m × Z
D = 2.5 mm × 40
D = 100 mm
Therefore, the pitch diameter of a spur gear with 40 teeth and a module of 2.5 mm is 100 mm.

Why Pitch Diameter is Crucial
The pitch diameter is not just a theoretical value; it has immense practical significance in gear system design:
- Center Distance: For two meshing gears, the center distance between their shafts is simply the sum of their pitch radii (half of their pitch diameters). Accurate pitch diameter calculation ensures proper meshing and avoids issues like backlash or jamming.
- Gear Ratio: While directly related to the number of teeth, pitch diameters also provide a way to visualize the effective rolling circles that transmit power.
- Interchangeability: Standardized modules ensure that gears with the same module and different numbers of teeth can mesh correctly if designed to the same pressure angle.
In conclusion, calculating the pitch diameter of a spur gear is a fundamental task in mechanical engineering. By understanding the module and number of teeth, engineers can accurately determine this critical dimension, ensuring efficient and reliable operation of gear trains.







